Feedforward neural networks (FNN) Deep Learning - Part 1

Contributors

Authors: Kaivan Kamali

Questions

• What is a feedforward neural network (FNN)?

• What are some applications of FNN?

Objectives

• Understand the inspiration for neural networks

• Learn activation functions & various problems solved by neural networks

• Discuss various loss/cost functions and backpropagation algorithm

• Learn how to create a neural network using Galaxy’s deep learning tools

• Solve a sample regression problem via FNN in Galaxy

Requirements

• tutorial Hands-on: Introduction to deep learning

What is an artificial neural network?

Speaker Notes

What is an artificial neural network?

Artificial Neural Networks

• ML discipline roughly inspired by how neurons in a human brain work
• Huge resurgence due to availability of data and computing capacity
• Various types of neural networks (Feedforward, Recurrent, Convolutional)
• FNN applied to classification, clustering, regression, and association

Inspiration for neural networks

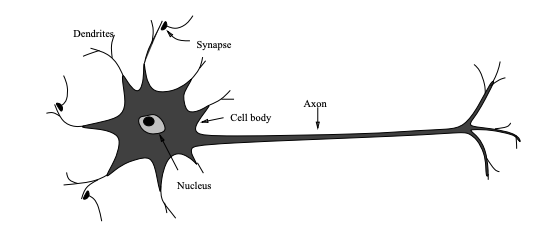
• Neuron a special biological cell with information processing ability
  • Receives signals from other neurons through its dendrites
  • If the signals received exceeds a threshold, the neuron fires
  • Transmits signals to other neurons via its axon
• Synapse: contact between axon of a neuron and denderite of another
  • Synapse either enhances/inhibits the signal that passes through it
  • Learning occurs by changing the effectiveness of synapse

Celebral cortex

• Outter most layer of brain, 2 to 3 mm thick, surface area of 2,200 sq. cm
• Has about 10^11 neurons
  • Each neuron connected to 10^3 to 10^4 neurons
  • Human brain has 10^14 to 10^15 connections

Celebral cortex

• Neurons communicate by signals ms in duration
  • Signal transmission frequency up to several hundred Hertz
  • Millions of times slower than an electronic circuit
  • Complex tasks like face recognition done within a few hundred ms
  • Computation involved cannot take more than 100 serial steps
• The information sent from one neuron to another is very small
  • Critical information not transmitted
  • But captured by the interconnections
• Distributed computation/representation of the brain
  • Allows slow computing elements to perform complex tasks quickly

Perceptron

Learning in Perceptron

• Given a set of input-output pairs (called training set)
• Learning algorithm iteratively adjusts model parameters
  • Weights and biases
• So the model can accurately map inputs to outputs
• Perceptron learning algorithm

Limitations of Perceptron

• Single layer FNN cannot solve problems in which data is not linearly separable
  • E.g., the XOR problem
• Adding one (or more) hidden layers enables FNN to represent any function
  • Universal Approximation Theorem
• Perceptron learning algorithm could not extend to multi-layer FNN
  • AI winter
• Backpropagation algorithm in 80’s enabled learning in multi-layer FNN

Multi-layer FNN

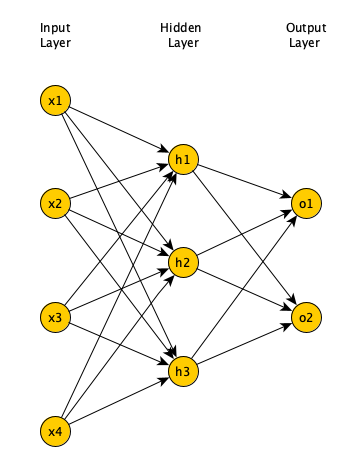
• More hidden layers (and more neurons in each hidden layer)
  • Can estimate more complex functions
  • More parameters increases training time
  • More likelihood of overfitting

Activation functions

Supervised learning

• Training set of size m: { (x^1,y^1),(x^2,y^2),…,(x^m,y^m) }
  • Each pair (x^i,y^i) is called a training example
  • x^i is called feature vector
  • Each element of feature vector is called a feature
  • Each x^i corresponds to a label y^i
• We assume an unknown function y=f(x) maps feature vectors to labels
• The goal is to use the training set to learn or estimate f
  • We want the estimate to be close to f(x) not only for training set
  • But for training examples not in training set

Classification problems

Output layer

• Binary classification
  • Single neuron in output layer
  • Sigmoid activation function
  • Activation > 0.5, output 1
  • Activation <= 0.5, output 0
• Multilabel classification
  • As many neurons in output layer as number of classes
  • Sigmoid activation function
  • Activation > 0.5, output 1

  • Activation <= 0.5, output 0

Output layer (Continued)

• Multiclass classification
  • As many neurons in output layer as number of classes
  • Softmax activation function
  • Takes input to neurons in output layer
  • Creates a probability distribution, sum of outputs adds up to 1
  • The neuron with the highest proability is the predicted label
• Regression problem
  • Single neuron in output layer
  • Linear activation function

Loss/Cost functions

• During training, for each training example (x^i,y^i), we present x^i to neural network
  • Compare predicted output with label y^1
  • Need loss function to measure difference between predicted & expected output
• Use Cross entropy loss function for classification problems
• And Quadratic loss function for regression problems
  • Quadratic cost function is also called Mean Squared Error (MSE)

Cross Entropy Loss/Cost functions

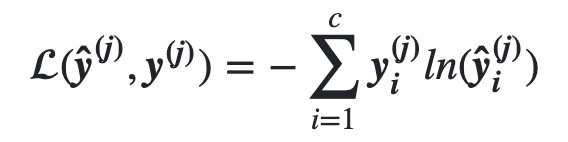
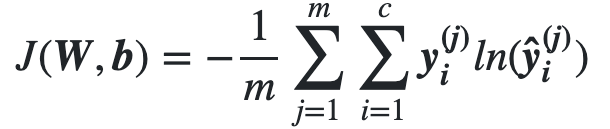
Quadratic Loss/Cost functions

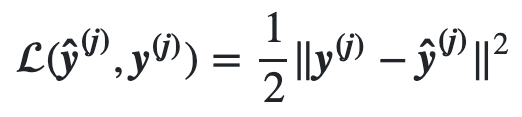
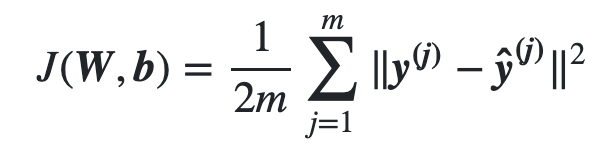
Backpropagation (BP) learning algorithm

• A gradient descent technique
  • Find local minimum of a function by iteratively moving in opposite direction of gradient of function at current point
• Goal of learning is to minimize cost function given training set
  • Cost function is a function of network weights & biases of all neurons in all layers
  • Backpropagation iteratively computes gradient of cost function relative to each weight and bias
  • Updates weights and biases in the opposite direction of gradient
  • Gradients (partial derivatives) are used to update weights and biases
  • To find a local minimum

Backpropagation error

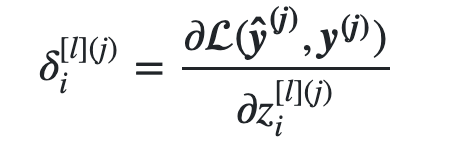
Backpropagation formulas

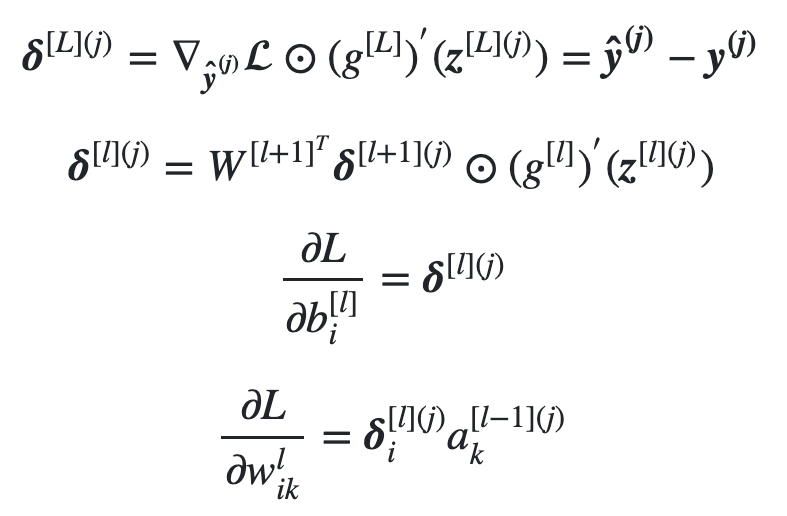
Types of Gradient Descent

• Batch gradient descent
  • Calculate gradient for each weight/bias for all samples
  • Average gradients and update weights/biases
  • Slow, if we have too many samples
• Stochastic gradient descent
  • Update weights/biases based on gradient of each sample
  • Fast. Not accurate if sample gradient not representiative
• Mini-batch gradient descent
  • Middle ground solution
  • Calculate gradient for each weight/bias for all samples in batch
    • batch size is much smaller than training set size
  • Average batch gradients and update weights/biases

Vanishing gradient problem

• Second BP equation is recursive
  • We have derivative of activation function
  • Calc. error in layer prior to output: 1 mult. by derivative value
  • Calc. error in two layers prior output: 2 mult. by derivative values
• If derivative values are small (e.g. for Sigmoid), product of multiple small values will be a very small value
  • Since error values decide updates for biases/weights
  • Update to biases/weights in first layers will be very small
    • Slowing the learning algorithm to a halt
  • The reason Sigmoid not used in deep networks
    • Why ReLU is popular in deep networks

Car purchase price prediction

• Given 5 features of an individual (age, gender, miles driven per day, personal debt, and monthly income)
  • And, money they spent buying a car
  • Learn a FNN to predict how much someone will spend buying a car
• We evaluate FNN on test dataset and plot graphs to assess the model’s performance
  • Training dataset has 723 training examples
  • Test dataset has 242 test examples
  • Input features scaled to be in 0 to 1 range

For references, please see tutorial’s References section

• Galaxy Training Materials (training.galaxyproject.org)

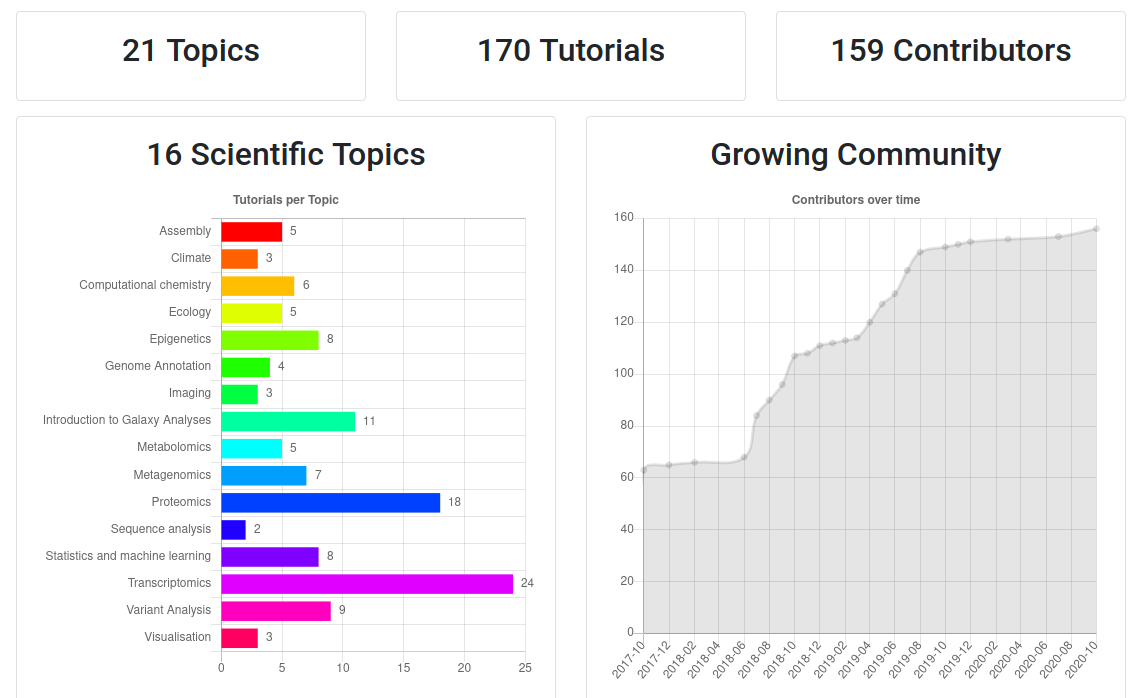
Speaker Notes

• If you would like to learn more about Galaxy, there are a large number of tutorials available.
• These tutorials cover a wide range of scientific domains.

Getting Help

• Help Forum (help.galaxyproject.org)

  

• Gitter Chat

  • Main Chat
  • Galaxy Training Chat
  • Many more channels (scientific domains, developers, admins)

Speaker Notes

• If you get stuck, there are ways to get help.
• You can ask your questions on the help forum.
• Or you can chat with the community on Gitter.

Join an event

• Many Galaxy events across the globe
• Event Horizon: galaxyproject.org/events

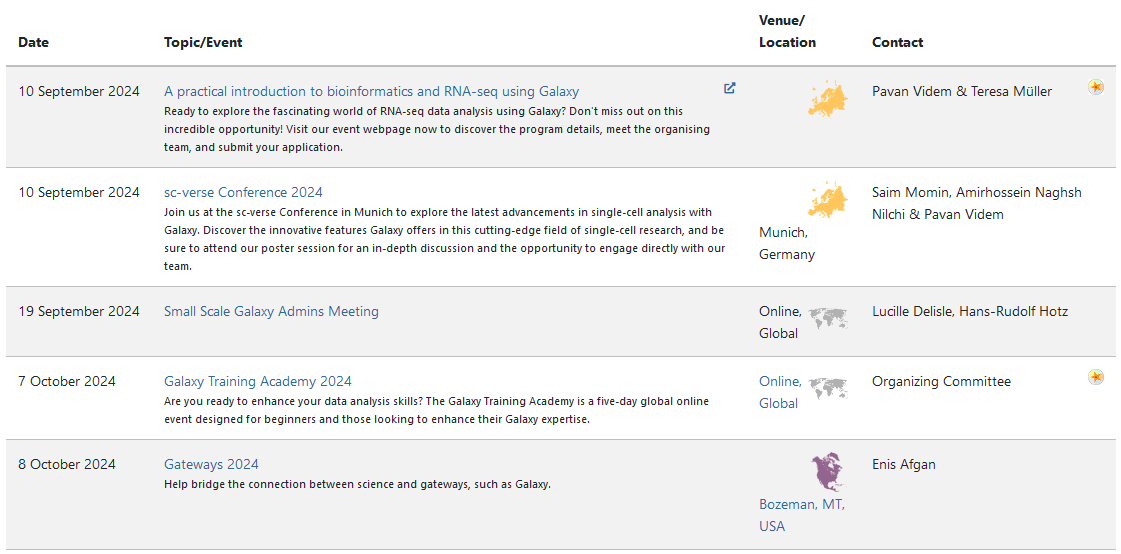
Speaker Notes

• There are frequent Galaxy events all around the world.
• You can find upcoming events on the Galaxy Event Horizon.

Thank you!